Un mundo de Voronói
Newsletter #98 – 2024/01/21
Buen martes a todos,
Anoche me acosté pensando en un dato curioso que hoy me apetece compartir1. ¿Alguna vez habéis pensado que el hielo puede considerarse una roca? La geología lo tiene claro: la roca es cualquier material sólido de origen natural formado por una asociación de minerales o por uno solo, que constituye una parte importante de la corteza terrestre2. Así que sí, el hielo, cuando aparece de forma natural sobre la superficie de la tierra, se trata de una roca.
Ahora lo verdaderamente inquietante. Si el hielo es una roca, ¿entonces el agua es lava? El magma son los minerales en estado líquido cuando están en la parte interior de un planeta, mientras pasa a llamarse lava cuando sucede en la superficie. Si nos ceñimos exclusivamente a esto, entonces el agua es definitivamente lava. Aun así, podríamos exigir que ese material líquido ha de pasar del interior del planeta a su superficie, tal y como sucede en el caso de los volcanes. Incluso con esa limitación, aún tendríamos el caso límite de los géiseres, una indudable fuente de agua-lava.
Esta idea no tiene nada que ver con lo que os voy a contar, del mismo modo que no tenía nada que ver lo que tenía pensado contar inicialmente3. El tema de hoy serán las regiones de Voronói, y cómo sería una administración territorial definida por ellas.
Los diagramas de Voronói
Los diagramas de Voronói, también llamados polígonos de Thiessen4, son algo relativamente simple de explicar, para lo que nos tienen acostumbrados las matemáticas. Si suponemos un espacio con puntos dispersos por él, las regiones de Voronói son los espacios compuestos por puntos que se encuentran más cerca de un punto común que de ningún otro. Dicho de una forma más simple, el espacio cuyo punto más cercano, de todos los definidos, es común.
Como bien es sabido, a los matemáticos les apasiona la complejidad, así que todo esto tiene un corpus teórico mucho más arduo de lo que soy capaz de cubrir de forma fidedigna. Tal y como lo definió Gueorgui Voronói en 1908, las regiones de Voronói pueden existir en espacios de N dimensiones, aunque para facilitar la comprensión, pensemos que esto aplica a una dimensión (segmentos en una línea), a dos dimensiones (polígonos en un plano) y a tres dimensiones (poliedros en el espacio).
Otra cuestión interesante es la definición de distancia. Dentro de la teoría matemática se pueden determinar múltiples formas de calcular una distancia, y esto puede aplicarse a las regiones de Voronói. Lo primero que pensamos todos es que distancia únicamente hay una, que es la que une dos puntos por una línea recta. Pero si lo maduramos un poco más, enseguida nos daremos cuenta de que, en nuestro día a día, ya trabajamos con varias distancias al movernos por la faz de la Tierra: la distancia en línea recta, la distancia por carretera, o la distancia en transporte público.
En el mapa de arriba podéis ver cómo las regiones de Voronói cambian en función de la distancia que se elija. A la izquierda, los polígonos se definen por el área que está más cerca de cada uno de los puntos definidos en línea recta, lo que se llama distancia euclídea. A la derecha, se utiliza la distancia Manhattan, con la que se establece una cuadrícula subyacente y la distancia se establece siguiendo los caminos de dicha cuadrícula.
Cómo se calcula la distancia es relevante, y eso lo vamos a ver a continuación con un mapa de España.
Regiones de Voronói en España
La división territorial de España en provincias fue obra de Javier de Burgos, en el año 18335. Desde entonces, las provincias han variado ligeramente y tan solo ha habido una división, la de la provincia de Canarias en 1927. La premisa inicial, copiada de los franceses, es que todo el territorio de la provincia tendría que ser capaz de llegar a la capital en menos de un día a caballo. Esto facilitaría la gobernanza y la comunicación, desligándose de las provincias y demás regiones históricas de España.
A veces sorprende que la división provincial de España se haya mantenido durante 200 años, pero la razón es simple: era una división buena. Esa premisa copiada a los franceses, de algún modo, servía a modo de distancia para definir unas regiones de Voronói en las que dividir y administrar el territorio del estado. Desde luego que esta división no es perfecta, pero si sobreponemos los polígonos de Voronói sobre un mapa provincial de España (únicamente centrándonos en la España peninsular), nos daremos cuenta de lo bien que se hizo.
Como es esperable, provincias como Badajoz o Zaragoza quedan en evidencia, pero en líneas generales las fronteras no se sitúan muy lejos de su ideal de Voronói. Badajoz acusa que la capital linde con Portugal, por lo que no tiene la posición central esperada de una capital que, posiblemente, habría tenido más sentido en Mérida. En el caso de Zaragoza, su tamaño la delata, con zonas de la provincia que están más cerca de todas las provincias circundantes.
Las premisas de Javier de Burgos, al definir las provincias, no tuvieron en cuenta la distancia recta, sino la distancia a caballo. Si tomamos una variación de esas premisas y calculamos la distancia en coche, ¿qué mapa nos resultaría?
Este otro mapa es mucho más interesante que el anterior. Manteniendo la integridad de todos los municipios, se calcula qué capital de provincia está más cerca de cada uno de ellos y, de este modo, se establecen los nuevos polígonos de Voronói. Las diferencias no son excesivas respecto al mapa anterior, aunque en esta ocasión todas las cordilleras ejercen de frontera física, asemejando las nuevas regiones a las provincias actuales.
Una cuestión que he obviado deliberadamente es si las provincias peninsulares deberían haber sido 48 o más. Para poder evaluar eso de forma rigurosa, tenemos que entender cuál es la distancia que separa cada uno de los municipios del país de una capital. El mapa a continuación, realizado por Aparovich, al igual que el anterior, muestra la distancia a una capital de provincia desde cada municipio, representando cada color una distancia de diez minutos.
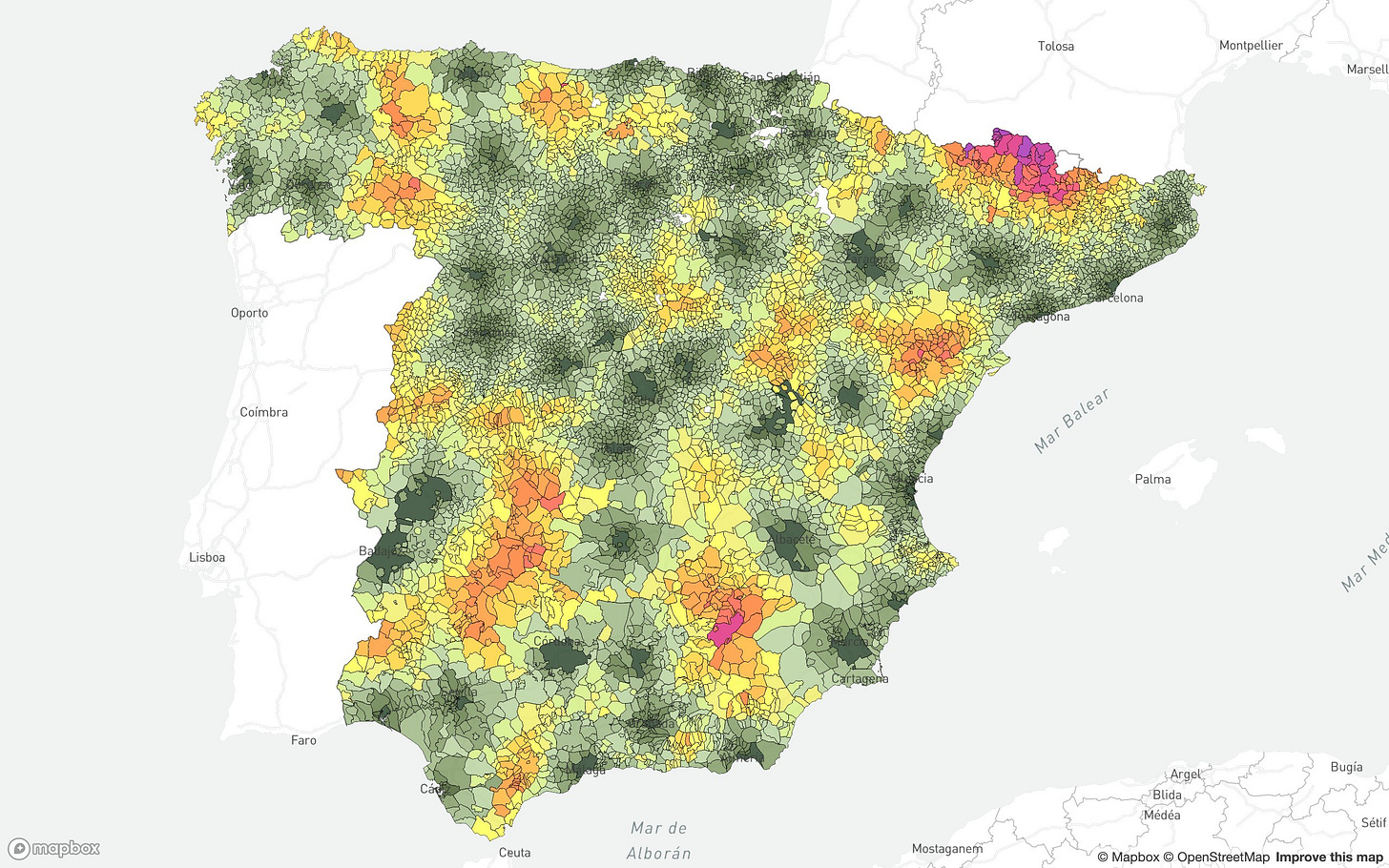
Los municipios que están peor situados son los del Pirineo de Lleida, en el noreste, y los de la Sierra de Cazorla, en el suroeste. En ambos lugares, se puede tardar hasta una hora y media en coche hasta llegar a la capital de provincia más cercana. En circunstancias semejantes se sitúa la frontera entre las comunidades de Extremadura y Castilla-La Mancha, así como la frontera entre Galicia, Asturias y Castilla y León. Todas estas regiones tienen en común que son abruptas y actualmente poco pobladas, por lo que sería difícil justificar una nueva provincia, quizá con la única excepción de Ponferrada, en la provincia de León.
Un mundo de Voronói
Después de divagar por las regiones de Voronói de España (y algo más), he dejado para el final un puñado más de mapas que os gustarán. Todos ellos describen cómo serían otras partes del mundo si las capitales y las regiones de Voronói fueran responsables de determinar las fronteras.
Empecemos con Europa.
Aquí se nota rápidamente que las fronteras de Europa, como las de ningún otro continente del mundo, no son planificadas. Esta es la razón por la que, a diferencia del caso de España, el territorio asociado con cada capital cambia radicalmente. Lo primero que llama la atención es cómo todas las pequeñas naciones-estado de Europa ganan mucho territorio. Andorra, Malta, San Marino, Liechtenstein o Mónaco son los mejores ejemplos. En el lado opuesto nos topamos como algunos de los grandes países del continente ven mermado su territorio a menos de una cuarta parte, como es el caso de Francia, Italia, Suecia o Rusia.
Ahora vamos a por los Estados Unidos.
La historia de los estados que forman la federación estadounidense es más cercana a los países de Europa que a las provincias de España. No hubo una planificación real, al menos no al nivel de las provincias de España, razón por la que existen notables diferencias entre algunos estados y la región de Voronói asociada a su capital. Quizá lo que salva que no sea tan radical es cómo se buscó que las capitales estatales estadounidenses no se correspondieran con la ciudad más grande y se localizaran en zonas estratégicas del estado. Que Albany sea la capital de Nueva York, permite que tenga mucho más territorio que si hubiera sido la ciudad de Nueva York. Algo semejante se puede decir de California y Sacramento o de Florida y Tallahassee.
Para finalizar, veamos un mapa mundial de Voronói.
Aquí ya hay muchas cosas que comentar. Como hemos dicho en el caso de Europa, las fronteras estatales no están planificadas, por lo que cualquier intento de redefinir las fronteras mediante regiones de Voronói será un cambio fundamental. De forma evidente, casi todos los grandes países se convierten en grandes perdedores, como es el caso de Rusia, Estados Unidos, Brasil, China o Australia. Canadá salva los papeles bastante dignamente y México recupera gran parte de su territorio histórico.
Muchos países son los que, sorprendentemente, salen ganando con creces. Ese es el caso de Nueva Zelanda y su conquista de la Antártida, o de Islandia, que se hace con Groenlandia y todo el norte de Canadá. Kazajistán, Mongolia, Corea del Norte y Japón se reparten el inmenso territorio asiático de Rusia. Chile conquista los Andes y se hace con toda la Patagonia, mientras que Argentina se queda fuertemente mermada por lo escorado que está situado Buenos Aires.
Podría comentar los detalles durante mucho más tiempo, pero en su lugar os voy a recomendar que visitéis este gran mapa interactivo de Jason Davies en el que se puede explorar las regiones de Voronói del mundo a todo detalle. Si os aburrís mucho, también os recomiendo que echéis otro vistazo a este otro mapa de Jason Davies donde utiliza como puntos de referencia los aeropuertos del mundo.
Las noticias de los últimos días me generan algo de ansiedad, y no me apetece esparcir esa ansiedad.
Los nombres vienen del primero que los definió, Gueorgui Voronói, en 1908, y de quien los aplicó al ámbito de la meteorología, Alfred H. Thiessen, en 1911.
Si os interesa saber la división provincial anterior de España, hablé sobre ella hace tiempo en este artículo: Tomás López y el primer atlas detallado de España (1804)
¡Gracias, maestro!
Fantástico, como siempre. No dejo de aprender. Bravo.