Una cabeza para mostrar la distorsión de los mapas
Newsletter #66 – 2024/06/11
Buen martes a todos,
Hace algo más de un año, al poco de aterrizar en Substack, escribí una entrada sobre el hecho de que las distorsiones son necesarias en las proyecciones cartográficas. Aún estaba buscando el formato de la newsletter y precisamente aquella fue la primera que tenía una coherencia de principio a fin. Disfruté mucho escribiéndolo y, de algún modo, fue el primer paso para que esta publicación semanal se convirtiera en lo que es a día de hoy.
A modo de homenaje, hoy quiero recuperar las distorsiones en las proyecciones cartográficas junto a una idea sobre la que escribí en mi difunto blog1. Se trata de una imagen que se incluía en un artículo que apareció en Scienfic American en diciembre de 1921, hace más de 100 años, en el que se usaba una cabeza para ayudar a visualizar las mentiras detrás de los mapas.
El trasfondo del artículo
Explicar la complejidad de las distorsiones que aparecen al trasladar una esfera a un plano es complicado, sobre todo si se busca que tenga sentido para todo el mundo. La geometría y la trigonometría es una parte de las matemáticas que se suele atragantar durante los años de instituto, así que no debe sorprender a nadie que un ejemplo práctico también sea difícil de entender.
Carl H. Claudy era consciente de este problema cuando redactó su artículo Otro nombre del mapa es Ananías2. Ananías de Damasco fue un personaje bíblico que murió de forma fulminante después de que Pedro le pusiera en evidencia por haber mentido a dios. No tengo constancia de que este personaje se use como referencia de forma común en castellano, pero en inglés sí que se utiliza de vez en cuando para referirse a un mentiroso compulsivo. Y eso era lo que quería dejar claro Claudy en su artículo: Todos los mapas dicen solo una parte de la verdad. Todos los mapas plano, en parte, falsifican los hechos.
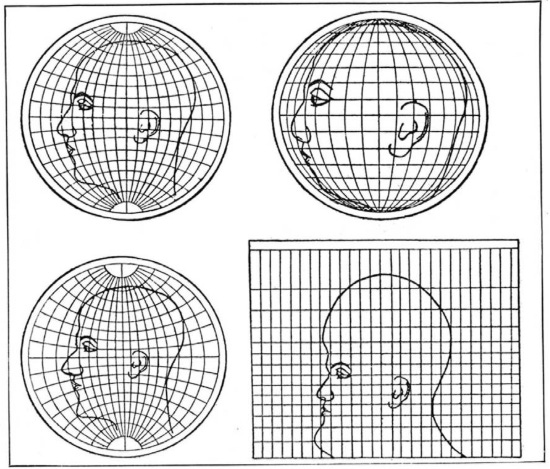
Para no caer en una explicación matemática compleja, Claudy optó por utilizar una cabeza. Puede parecer un burdo ejemplo, pero la verdad es que empleó el tiempo necesario para que las distorsiones fueran fieles. Con la misma profesionalidad con la que un cartógrafo dibuja un mapa siguiendo las pautas de la proyección matemática elegida, Claudy transformó una cabeza para mostrar cómo algunas de las proyecciones más populares distorsionan la realidad.
Las cabezas de Claudy
Las proyecciones cartográficas que representan la Tierra en un plano distorsionan la realidad. De sobra es conocido el caso de la proyección Mercator, la cual distorsiona la forma y el tamaño de los elementos del mapa en función de su latitud. Pero cualquier otra proyección que tomemos tendrá alguna distorsión. Es uno de los grandes problemas de que el planeta en el que vivimos, la Tierra, se asemeje mucho a una esfera y la esfera sea un cuerpo no desarrollable. O dicho de forma sencilla, que no se pueda extenderse en un plano.
El punto de inicio que tomó Claudy fue una proyección globular sobre la que pintó una cabeza. Esta proyección se utilizó históricamente por su gran facilidad para dibujarse, a pesar de su limitado valor matemático. Se asemeja mucho a una proyección acimutal equidistante y, por ello, era de gran utilidad para medir distancias entre dos puntos del planeta.
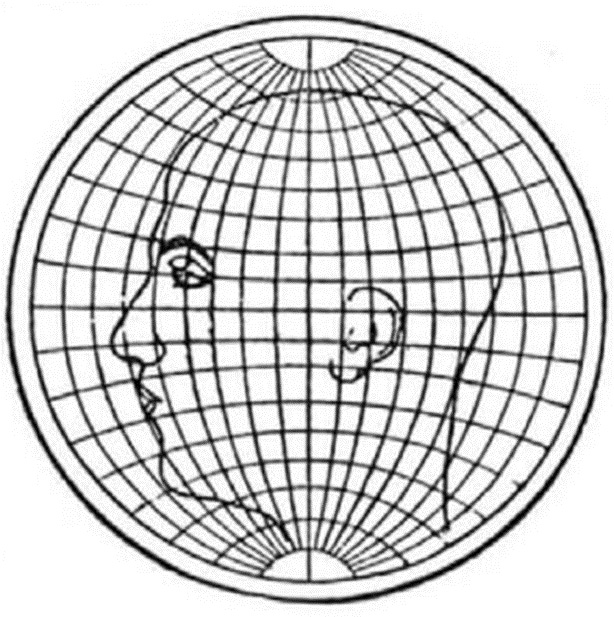
La cabeza está dibujada sin distorsión sobre este tipo de proyección porque necesitamos un punto de referencia en la comparativa, pero no porque esta proyección no distorsione la realidad, ya que lo hace notablemente. Aunque sí que mantiene bien las distancias (es equidistante), falla mucho en las áreas (no es equivalente) y mucho en las formas y ángulos (no es conforme).
Al cambiar la proyección de globular a una proyección ortográfica vemos como nuestra cabeza cambia notablemente. Esta nueva proyección se caracteriza por mantener a la perfección la distancia a lo largo de las circunferencias que se trazan de forma concéntrica desde el centro del mapa, pero a cambio distorsiona áreas y formas, más cuanto más alejado del centro se esté. Si observamos la cabeza, vemos claramente como abomba su forma por la parte central, dejando las zonas exteriores empequeñecidas y deformadas.
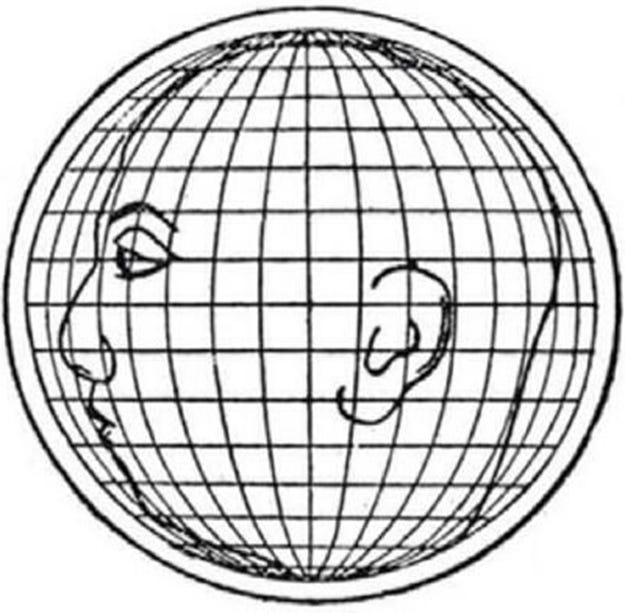
En realidad esta proyección representa lo que se observaría si viéramos la tierra desde el infinito, o al menos desde una distancia considerable. Es decir, si tomásemos una fotografía de la Tierra desde el Sol, el resultado sería, dejando de lado pequeñas imperfecciones, casi una proyección ortográfica.
Si ahora cambiamos la proyección globular inicial por una proyección estereográfica, vemos como nuestra cabeza vuelve a transformarse. En este caso tenemos como resultado una proyección conforme, que mantiene las formas, pero que distorsiona los otros dos pilares fundamentales de una proyección: las áreas y las distancias. A pesar de todas sus deficiencias, también tiene sus utilidades.
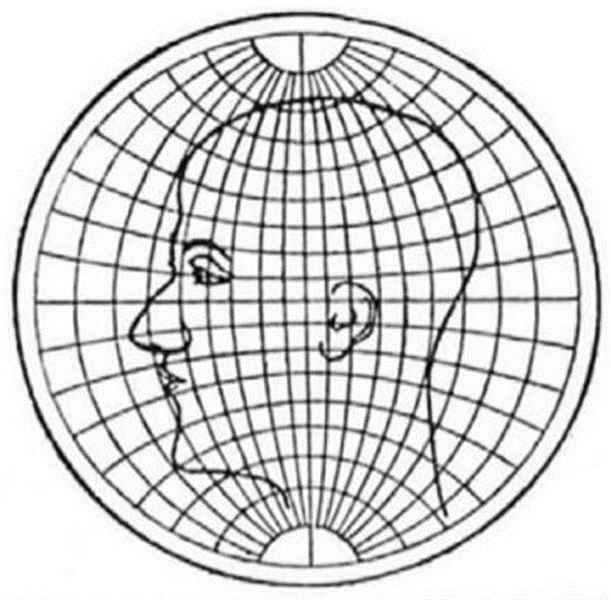
La proyección estereográfica es una de las pocas proyecciones que logra representar los círculos en la esfera como círculos en el plano. Esta peculiaridad es de utilidad cuando lo que se quiere es representar los cráteres de un satélite como la Luna. Precisamente por esto la proyección estereográfica se utiliza bastante en la cartografía de cuerpos del sistema solar, para así entender mejor las características de las zonas de impacto.
Por último, vamos a cambiar la proyección globular y convertirla en la proyección de Mercator, lo que nos resulta en una personificación de la aberración. La cabeza se ve distorsionada en forma y área mucho más que en cualquiera de las proyecciones anteriores. La parte superior e inferior de la cabeza carecen prácticamente de cualquier tipo de valor visual, siendo irreconocible la presencia de un cuello o un cráneo normal.
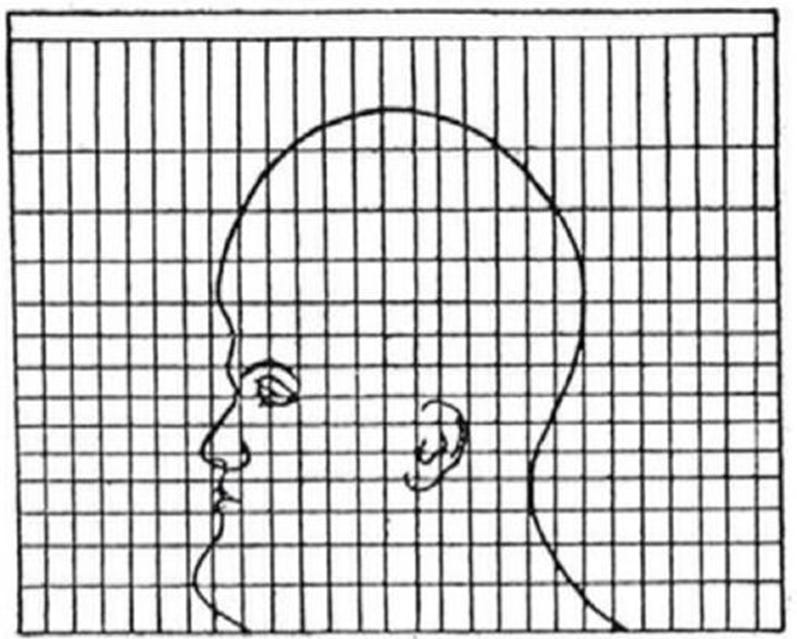
Pero, si la proyección Mercator es tan deplorable, ¿por qué se ha sido la principal proyección utilizada durante prácticamente cuatro siglos? No, no es porque estamos ante un sistema opresor que pretende dar importancia al hemisferio norte, tal y como decía Peters, sino porque esta proyección es una proyección conforme, por lo que preserva el rumbo. Si nos situamos en un punto del mapa con un navío y trazamos una línea siguiendo una dirección (noreste, por ejemplo), si mantenemos esa dirección de forma constante recorreremos la línea que hemos trazado en el mapa. Esta característica era clave para la navegación hasta los avances tecnológicos de las últimas décadas.
Muchas gracias a todos los que os pasasteis por la Feria del Libro de Madrid el pasado domingo, superó con creces todas mis expectativas.
Si os sigue picando el gusanillo sobre el libro, aquí conté más en detalle de qué trata.
No es el único difunto blog. Como muchos de los que estamos por aquí, hemos tenido bastantes blogs y sitios diversos en los que hemos publicado cosas en Internet. Además de Recuerdos de Pandora, también guardo un grato recuerdo de Cada día un Cantar, un blog en el que escribí durante un puñado de años sobre música… y que ya está totalmente desaparecido. Aunque sigue siendo el nombre de la lista de reproducción que actualizo regularmente en Spotify (y que me sirve de radio cuando no quiero pensar en qué escuchar).
El título original en inglés es A Map's Other Name is Ananias y se puede encontrar en la web de Scientific American, pero solo para suscriptores. Como ya han pasado más de cien años, os paso el PDF del artículo completo por aquí.



Cuando he leído el título, me esperaba que hubieran usado la forma aproximadamente esférica de una cabeza para extender la piel por completo y mostrar en la proyección de Mercator la verdadera distorsión que sufre una superficie esférica al disponerse en una forma rectangular. Aunque un poco desagradable, ese ejercicio habría resultado muchísimo más ilustrativo.
Siempre aprendiendo. Qué gusto