El problema de la costa de Gran Bretaña
Newsletter #83 – 2024/10/08
Buen martes a todos,
¿Alguna vez os habéis planteado cuánto mide la costa de España? Así, sin pensarlo mucho, seguramente es algo que se puede consultar en cualquier enciclopedia, del mismo modo que se puede encontrar el área, el punto más alto o la capital del país. De esta manera, buscando en The World Factbook1, la longitud de costa para España es de 4964 kilómetros.
Ya está, problema solucionado… ¿O no?
Si intentamos contrastar información, para asegurarnos de que The World Factbook no miente, podemos consultar otra fuente de referencia como la ONG World Resources Institute2. Ahí nos encontramos con un número distinto, 7268,1 kilómetros, ni más ni menos que un 46 % más que la medición proporcionada por The World Factbook.
Podría haber elegido una discrepancia entre dos fuentes, pero consultéis donde consultéis, os vais a encontrar con que los números no concuerdan, y si concuerdan es que unos han copiado de otros. La Wikipedia sube la cifra hasta los 7661 kilómetros3 y el Instituto Geográfico Nacional de España, que quiero considerar la más fiable en esta medida, eleva la longitud de la costa hasta 7879 kilómetros.
¿Sorprendidos? Pues así se quedó un matemático inglés allá por 1960, cuando se topó con el problema por primera vez.
El hallazgo de Lewis Fry Richardson
Lewis Fry Richardson fue un académico muy polivalente. Investigó en campos tan diversos como las matemáticas, la física o la psicología y, además, era un pacifista convencido. Richardson creía que con las matemáticas y la física aplicadas se podían encontrar patrones en el funcionamiento del mundo, para entender todo tipo de catástrofes y, de ese modo, encontrar formas de prevenirlas. De algún modo, esa forma de pensar explica la motivación que le llevó a estudiar meteorología y terminar creando uno de los primeros modelos para pronosticar del tiempo.

Esas inquietudes le llevaron a intentar entender, en 1961, si existía alguna relación entre la probabilidad de que dos países entrasen en guerra y la longitud común de su frontera. Al recopilar datos, se encontró que distintas fuentes proporcionaban datos dispares. Por ejemplo, España estimaba que su frontera con Portugal era de 1214 kilómetros, mientras que Portugal, por su parte, decía que eran solo 987 kilómetros. Podría ser una curiosidad sin más, pero cuando consultó la longitud de la frontera entre Países Bajos y Bélgica, también se encontró con dos valores diferentes: 380 y 449 kilómetros.
Esas discrepancias supusieron una sorpresa para Richardson, pero rápidamente se topó con una explicación: todo dependía de cómo se midiera la frontera. Si se utilizaba una regla de gran tamaño, inevitablemente muchos detalles no se medirían y la distancia total sería más corta. Por la contra, con una regla de menor tamaño, era posible entrar en más recovecos y, así, alcanzar una distancia total mayor.
Para ejemplificarlo, he medido en Google Maps la longitud de la frontera entre Bélgica y Países Bajos con segmentos de distinto tamaño. Tomando únicamente segmentos de 20 kilómetros, se obtiene una distancia aproximada de 259 kilómetros. Si en su lugar utilizamos segmentos de 10 kilómetros, la distancia final es de 315 kilómetros. Más distancia en el segundo caso, pero en ambos mucho menor que las distancias oficiales con las que se topó Richardson. Sin duda, gracias a que las medidas utilizaban una regla de un tamaño mucho menor a 10 kilómetros.
Richardson publicó este hallazgo en su artículo de 1961 “The problem of contiguity: An appendix to Statistics of Deadly Quarrels” (El problema de la contigüidad: un apéndice a las estadísticas de las peleas mortales)4 y extrapoló el problema a las costas que definen un país. Dentro de su estudio, demostraba algo que, a priori, puede resultar contraintuitivo: a medida que se disminuye el tamaño de la regla que se utilice para medir, la longitud de la costa aumenta sin ningún límite. Esto es lo que se conoce como el efecto Richardson5.
Mandelbrot y la costa de Gran Bretaña
Las fronteras entre dos países, al final, son unas líneas consensuadas entre los dos países que forman dicha frontera. Esto hace que los recovecos sean limitados y, al final, se pueda llegar a un consenso. Las costas, por su parte, son un resultado de millones de años de movimientos de placas tectónicas y la acción de los elementos, los entrantes y salientes son complejos y de tamaños que pueden llegar a ser de varios órdenes de magnitud inferior al tamaño total de la costa.
Benoît Mandelbrot se topó con el artículo de Richardson y decidió indagar en el problema matemático de las costas, publicando los resultados en su artículo de 1967 titulado “How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension” (¿Qué longitud tiene la costa de Gran Bretaña? Autosimilitud estadística y dimensión fraccionaria)6. En el congreso donde fue presentado, Mandelbrot preguntó a sus colegas sobre la longitud de la costa de Gran Bretaña. Algunos dieron una burda estimación, otros se refirieron a datos enciclopédicos, pero ninguno dio con la respuesta que Mandelbrot esperaba: infinito.
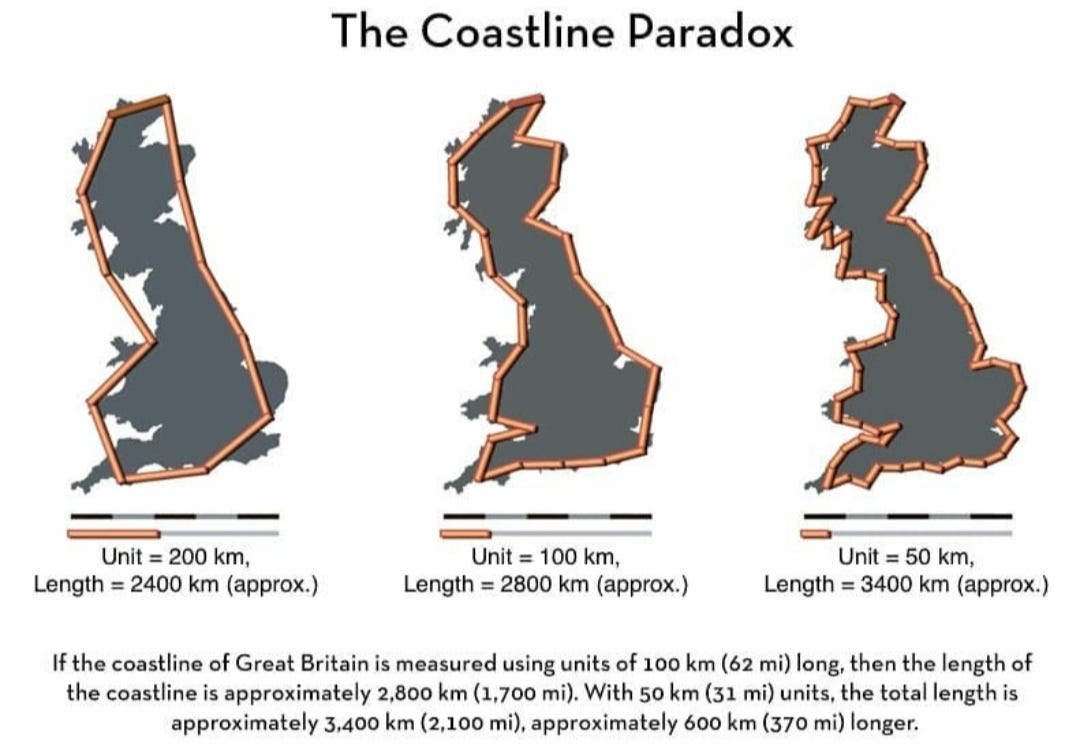
Los topógrafos, cuando se aventuran a medir la longitud de una línea costera, utilizan un metro o compás de longitud definida. Pongamos que se utilizan tramos rectos de 200 kilómetros para medir la costa de la isla de Gran Bretaña. El resultado que obtendrán será aproximadamente de 2400 kilómetros, tal y como muestra la imagen superior. Cualquiera puede determinar que esta aproximación es burda y harto de imprecisa. Entonces será mejor que tomemos un tramo recto de medición menor, 50 kilómetros, por ejemplo. En este caso, el resultado de la medición de la longitud de la costa será superior al caso anterior, 3400 kilómetros. La explicación es sencilla, ya que ahora hemos tenido la oportunidad de medir recodos que antes habían quedado totalmente obviados.
¿Pero es esta aproximación suficiente? Tal y como muestra la siguiente animación, claramente no.

Cuando el segmento de medida se reduce hasta 100 metros, la longitud total que nos encontramos es de 17.820 kilómetros, casi cinco veces más que cuando la medida de referencia es 50 kilómetros. Volviendo a los dos datos enciclopédicos que hemos tomado como referencia al principio, nos encontramos con que The World Factbook otorga al total del Reino Unido (Gran Bretaña, Irlanda del Norte y todas las islas menores) una línea de costa de 12.429 kilómetros, mientras que World Resources Institute se va a 19.717 kilómetros. Con esos datos en la mano, podemos inferir que la resolución de estas dos medidas, con casi total seguridad, supera los 100 metros.
Epílogo
El otro día, hablando sobre esto con Javier Jurado7, me comentó que hace unos años, en un examen de oposición en España, una de las cuestiones planteadas preguntaba cuál era la comunidad autónoma de la España peninsular con mayor kilómetros de costa8.
Os animo a que intentéis responder sin consultar en Internet la respuesta.
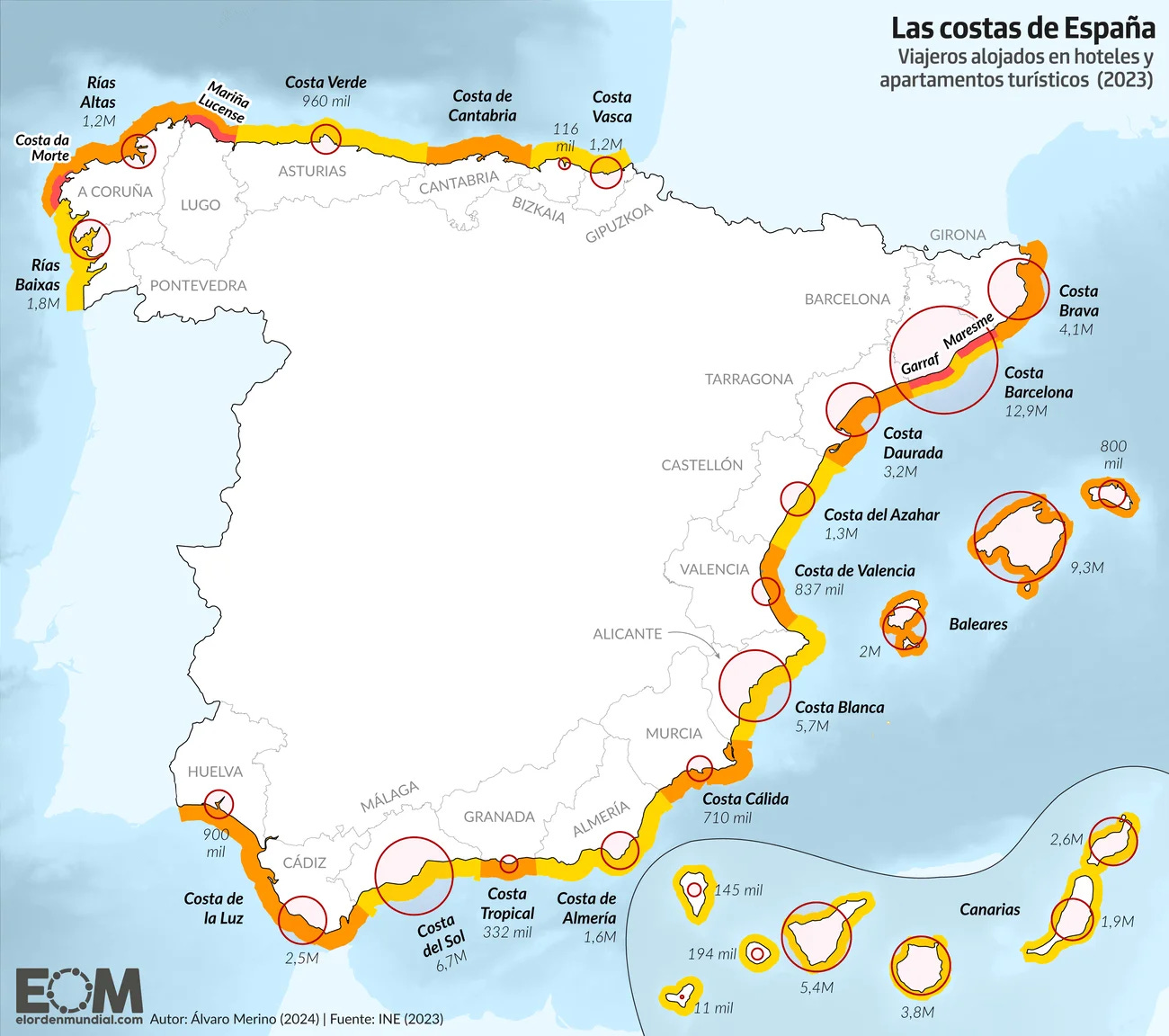
Para que no tengáis que subir arriba o buscar por Internet, os vuelvo a dejar el mapa de las costas de España.
Pero responded a la encuesta antes de ir más abajo.

A modo de curiosidad, he echado un rato en Google Maps para medir en segmentos de 20 kilómetros las costas de las cuatro comunidades, y estos son los resultados:
Andalucía: 663 kilómetros.
Cataluña: 360 kilómetros.
Comunidad Valenciana: 372 kilómetros.
Galicia: 447 kilómetros.
Entonces, Andalucía queda a la cabeza, seguida de Galicia, Comunidad Valenciana y Cataluña.
O bueno, más bien no. Los datos oficiales que proporciona el Instituto Geográfico Nacional varían ligeramente:
Andalucía: 910 kilómetros, un 37 % más.
Cataluña: 699 kilómetros, un 94 % más.
Comunidad Valenciana: 518 kilómetros, un 39 % más.
Galicia: 1498 kilómetros, un 235 % más.
Sí, las rías gallegas multiplican la longitud de su costa hasta el punto de hacerla mucho más larga que la costa de Andalucía, que en apariencia sería más extensa.
¿Habríais acertado esa pregunta del examen?
Yo habría fallado9.
El pasado 16 de abril se publicó mi primer libro, sobre la historia de la propaganda. Echad un vistazo si queréis más detalles… ¡Y corred la voz!
Y bueno, muchas gracias por la acogida. Se agradece.
The World Factbook es una publicación anual de la CIA con datos de todos los países del mundo.
Los datos de esta ONG son utilizados por muchas organizaciones estatales y supraestatales, como es el caso de la Agencia Europea del Medio Ambiente.
La Wikipedia en español, porque la holandesa se queda con los datos de la CIA y la alemana redondea hasta 8.000 kilómetros.
El artículo se publicó aquí. He intentado acceder a una copia del mismo, pero me ha sido imposible.
Esta afirmación la realizó sobre las costas, no sobre las fronteras. Lo explico un poco más adelante.
Que, por cierto, tenéis que pasaros sin falta por su newsletter para que veáis una cosa muy guay que acaba de anunciar hace unos días.
No sé si la pregunta era exactamente esa, pero la idea sí que queda plasmada.
A modo de curiosidad, una nota irrelevante más. Según los datos oficiales del Instituto Geográfico Nacional, la comunidad con más kilómetros de costa es Canarias, pero por poco.





A la hora de crear imágenes sintéticas para el cine, Loren Carpenter se enfrentó al mismo problema que quienes medían costas o fronteras a base de líneas: por muy cortos que fueran los segmentos o formas poligonales utilizados, la animación digital no lograba reflejar la realidad.
Gracias a la lectura de Mandelbrot, Carpenter empezó a pensar en algoritmos capaces de generar fractales, para hacer así más verosímiles las formas y contornos de nubes, montañas, volcanes, costas o planetas enteros creados por ordenador.
Los revolucionarios códigos de renderizado y modelado digital que programó superaron la dureza de los escenarios rollo “minecraft”, le valieron un Oscar y llevaron al éxito a su siguiente empresa: Pixar.
Muy interesante este artículo, Miguel, gracias por escribir sobre esto, es un tema que me atrae desde hace tiempo. Tengo notas a desarrollar para escribir sobre Mandelbrot y los fractales, es fascinante la cantidad de aplicaciones que se extrae de la noción de fractal (vi un viejo documental de la BBC sobre Mandelbrot que era interesantísimo, si doy con él lo comparto aquí).
Aquí viene muy al hilo el Copo de nieve de Koch, uno de los conceptos fractales originales, en el que los lados de un triángulo equilátero se subdividen sucesivamente y hasta el infinito formando una figura similar (claro) a un copo de nieve:
https://mathworld.wolfram.com/KochSnowflake.html