Este proyecto, que incluye esta newsletter y el catálogo de mapas, lleva tiempo y dedicación. Si quieres apoyarlo, suscríbete y compártelo. Si además quieres ayudar a que sea sostenible, considera una suscripción de pago. Esto te permitirá, entre otras cosas, acceso a los monográficos y los mapas del mes.
Buen viernes a todos,
No es la primera vez que hablo de la distribución de la población mundial, aunque es cierto que hace bastante que no lo hago. Hace un par de años, cuando por aquí aún pasaba poca gente, dediqué un par de entradas a la densidad de la población, por un lado, centrándome en la latitud y la longitud, y por otro en las distintas formas para mostrar mapas de densidad de población.
Lo que os traigo hoy es posible que os lo hayáis planteado en alguna ocasión. Incluso puede ser que os hayáis topado con algún mapa que intente solucionar este problema. La premisa es simple: ¿cuál es el círculo más pequeño que podemos dibujar que contenga a la mitad de la población mundial?
El círculo de Valeriepieris
Esta aventura comienza el 5 de mayo de 2013. Hasta ese momento, muchas personas a lo largo de la historia se han planteado cuáles son las regiones más pobladas del planeta, y cuáles son los lugares donde se concentra más población. Pero lo que no había hecho nadie es intentar encontrar el círculo mínimo que contuviera más de la mitad de la población mundial.
Aquel domingo, Ken Myers, usando el alias Valeriepieris, publicó la siguiente imagen en Reddit1, acompañada del siguiente comentario: Después de ver un mapa sobre la población de Indonesia, se me ha ocurrido esto.
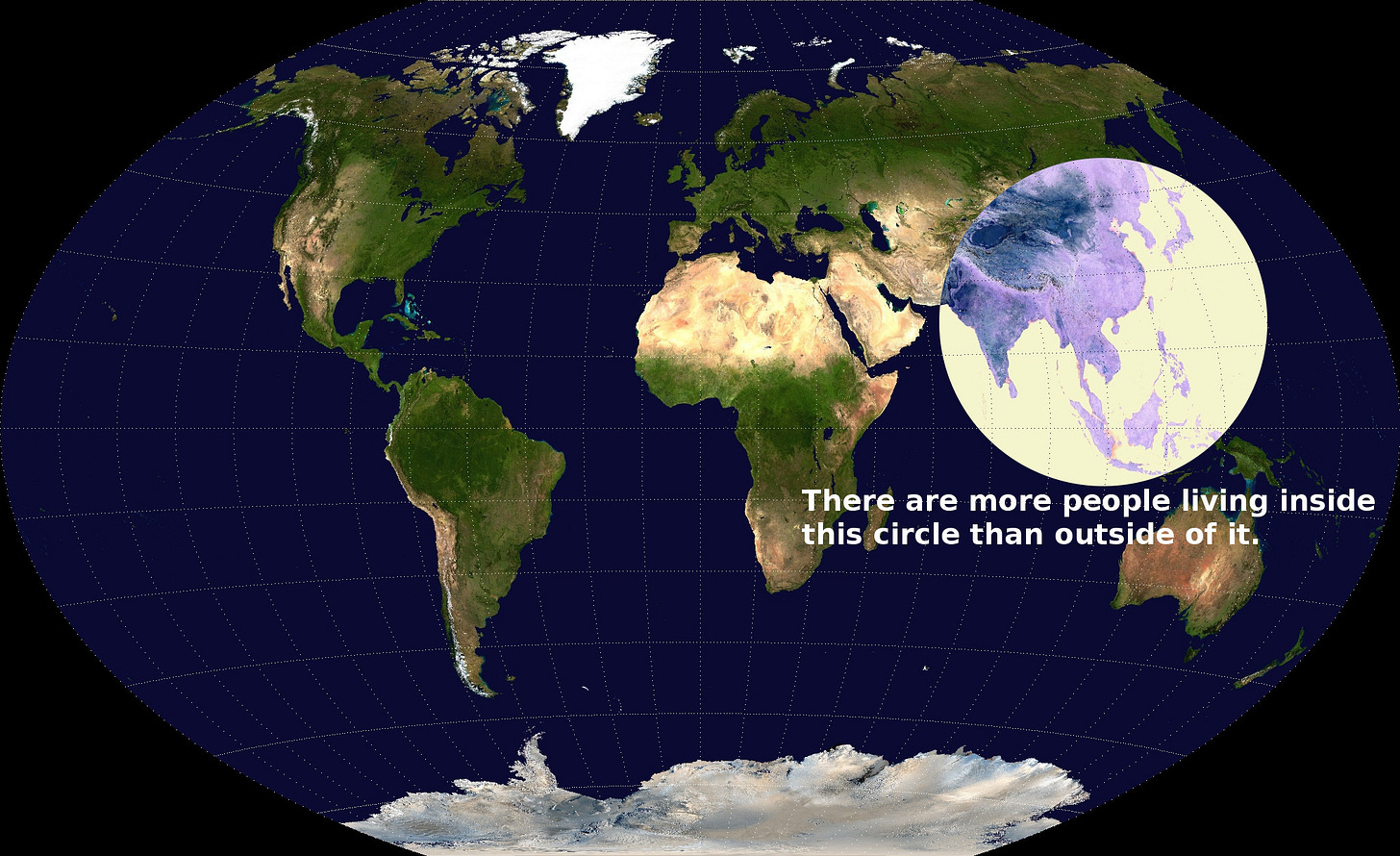
Todos sabemos que en esa región del mundo se encuentran los dos países más poblados, India y China, así como muchos otros países que cuentan con una población notable, como Japón, Filipinas, Vietnam, Bangladés o Indonesia. Las cuentas, con los datos de población en mayo de 2013, salían a la perfección. Había 3.637.830.357 personas dentro del círculo, lo que supone más de la mitad de los 7.100 millones de personas que había en todo el mundo2:
China: 1.349.585.838
India: 1.220.800.359
Indonesia: 251.160.124
Bangladés: 163.654.860
Japón: 127.253.075
Filipinas: 105.720.644
Vietnam: 92.477.857
Tailandia: 67.448.120
Myanmar: 55.167.330
Corea del Sur: 48.955.203
Nepal: 30.430.267
Malasia: 29.628.392
Corea del Norte: 24.720.407
Taiwán: 23.299.716
Sri Lanka: 21.675.648
Camboya: 15.205.539
Laos: 6.695.166
Mongolia: 3.226.516
Bután: 725.296
El autor no afirmó en ningún momento que ese era el círculo de menor tamaño que cumplía la condición. Simplemente, dijo que era sorprendente ver que dentro de ese círculo había más población que fuera, a pesar de ser una parte muy pequeña de la superficie de la Tierra3. Pero claro, el debate comenzó, ¿cuál es el círculo de menor tamaño que contiene la mitad de la población mundial?
El primer problema para solucionar esto, es aceptar que un mapa es una representación en el plano que varía en función de la proyección elegida4. Ken Myers utilizó la proyección de Robinson centrada en el meridiano de Greenwich y, en cierto modo, esa elección dictó que el círculo tuviera esa forma y ocupase esa región.
La corrección de Danny Quah
Dos años más tarde, en 2015, Danny Quah y Ken Teoh5 pasaron gran parte del verano jugando a encontrar el círculo de menor tamaño que contuviera la mitad de la población mundial. Para ello, tan solo hizo falta trabajar en un modelo matemático tridimensional, tomando siempre una circunferencia sobre la superficie terrestre, e incluyendo datos más granulares sobre la población que puebla cada punto.
Dadas las limitaciones de computación que había hace 10 años6, Quah tuvo que limitar los datos de población a cuadrados de 100 kilómetros de lateral, ya que los servidores de su universidad, la LSE, no conseguían completar el cálculo con más nivel de detalle.
El resultado fue el siguiente.
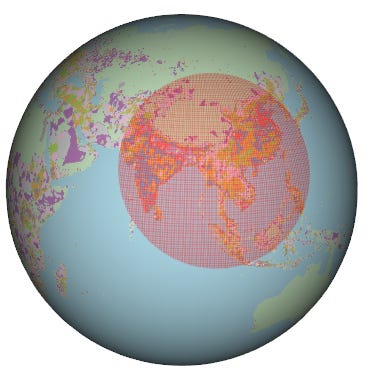
Mucha gente, incluido el propio Quah, se sorprendió de la gran aproximación que logró Ken Myers con un círculo trazado a ojo, tan solo teniendo en cuenta la población de cada país, y no de regiones concretas. Es cierto que hay algunas diferencias, como que este nuevo círculo excluye por completo a Japón y la mitad de Indonesia, aunque incorpora una mayor región de Pakistán y Asia Central.
El centro del círculo está situado en Mong Khet, al este de Myanmar, y tiene un radio de 3.300 kilómetros. En comparación, el círculo de Valeriepieris tiene un radio de 4.000 kilómetros y, sorprendentemente, está situado en China, pero justo al otro lado de la frontera con Myanmar.
El círculo de Yuxi
En 2022, Alasdair Rae7 volvió de nuevo a trabajar sobre la idea original de Ken Myers y buscó cuál de las 1.500 ciudades de mundo con más población tenía un círculo de 4.000 kilómetros a su alrededor con más habitantes. Eso sí, calculándolo sobre la superficie del geoide terrestre y con una granularidad de 1 kilómetro, mucho menor a la utilizada por Quah8.
La ciudad ganadora fue Yuxi, en China. Muy cerca del punto central del círculo de Valeriepieris.
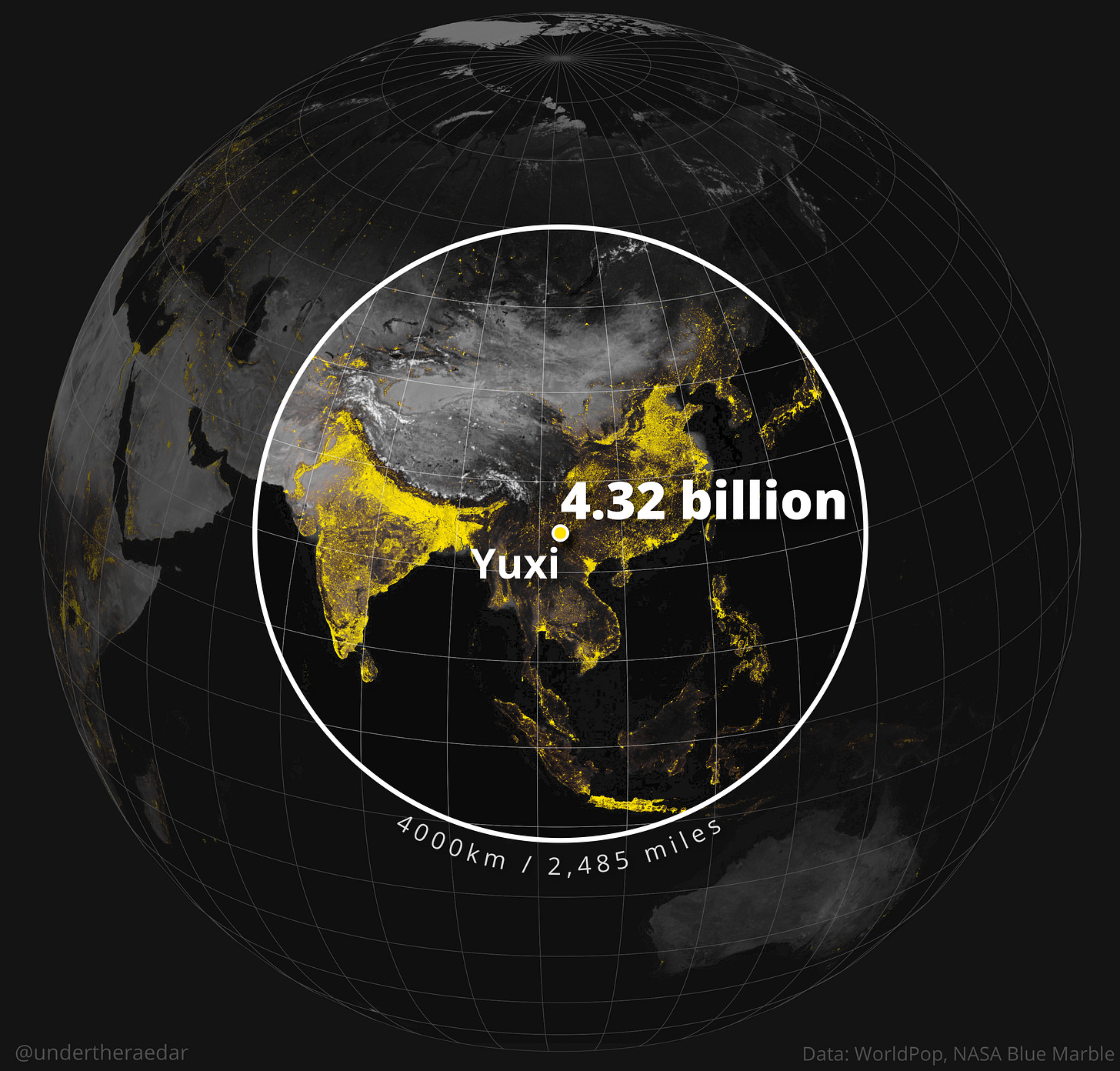
Tal y como cuenta Rae en el artículo que publicó junto a este mapa, los círculos de 148 ciudades superaban los 4.000 millones de habitantes, lo que en 2022 era la mitad de la población mundial9. La gran mayoría de esas ciudades están en China, aunque también hay ciudades en Vietnam, Myanmar, Laos, Bangladés, India e incluso Bután.
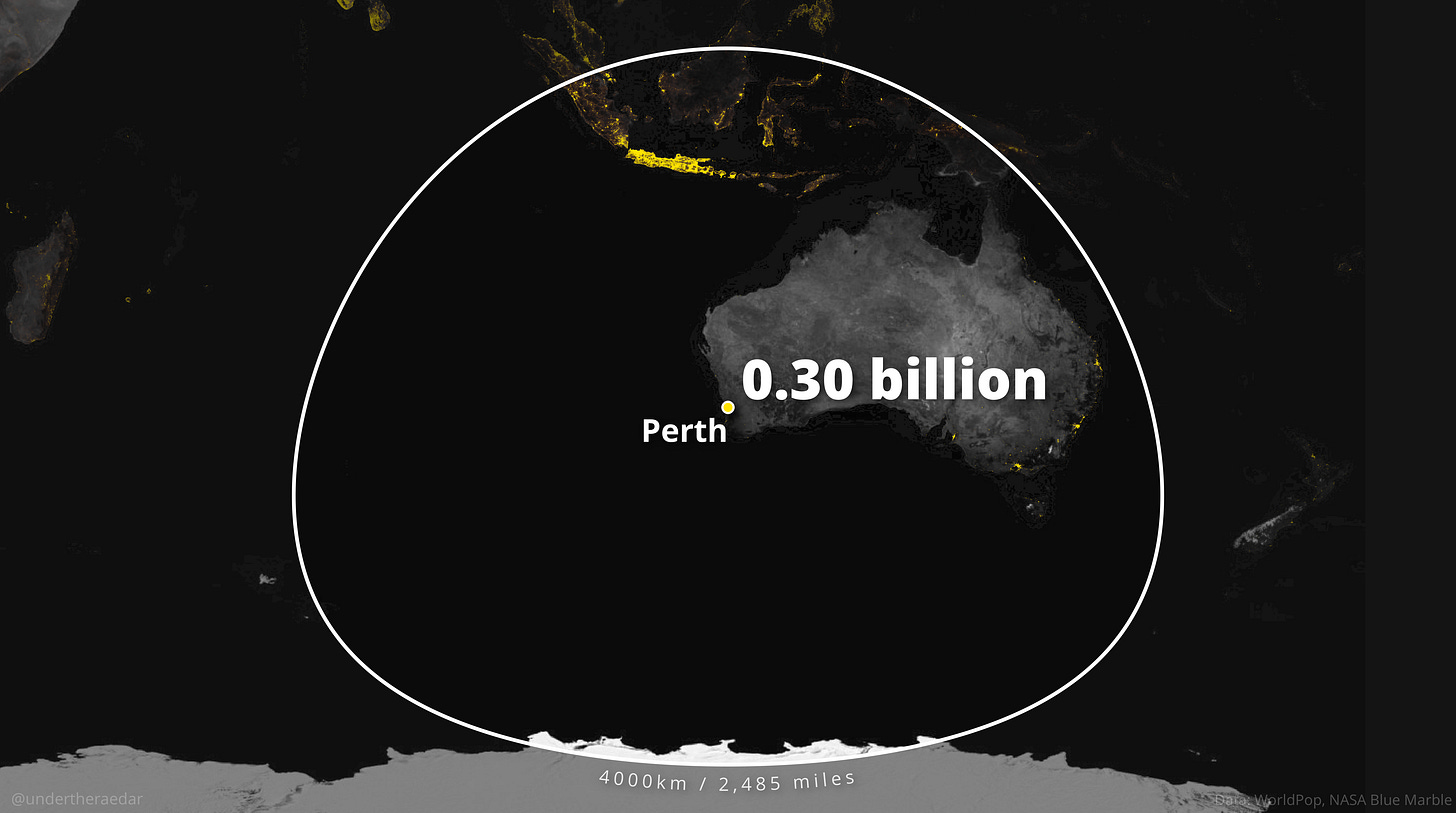
Como dato curioso, para ver los resultados de este mismo círculo en otros puntos del mundo, también compartió un buen puñado de mapas con una circunferencia de 4.000 kilómetros en torno a grandes ciudades. Aquí os dejo algunos ejemplos más.
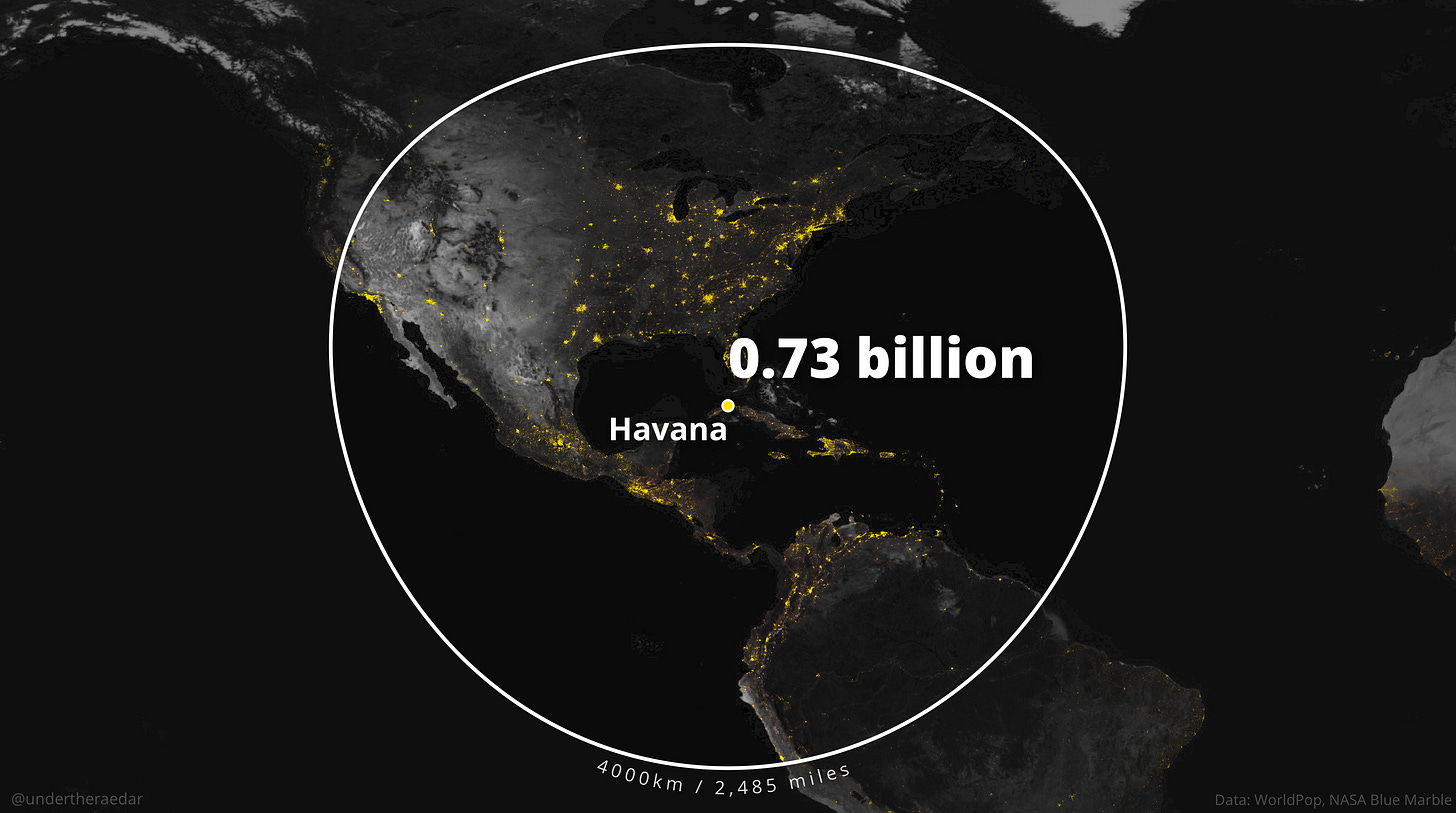
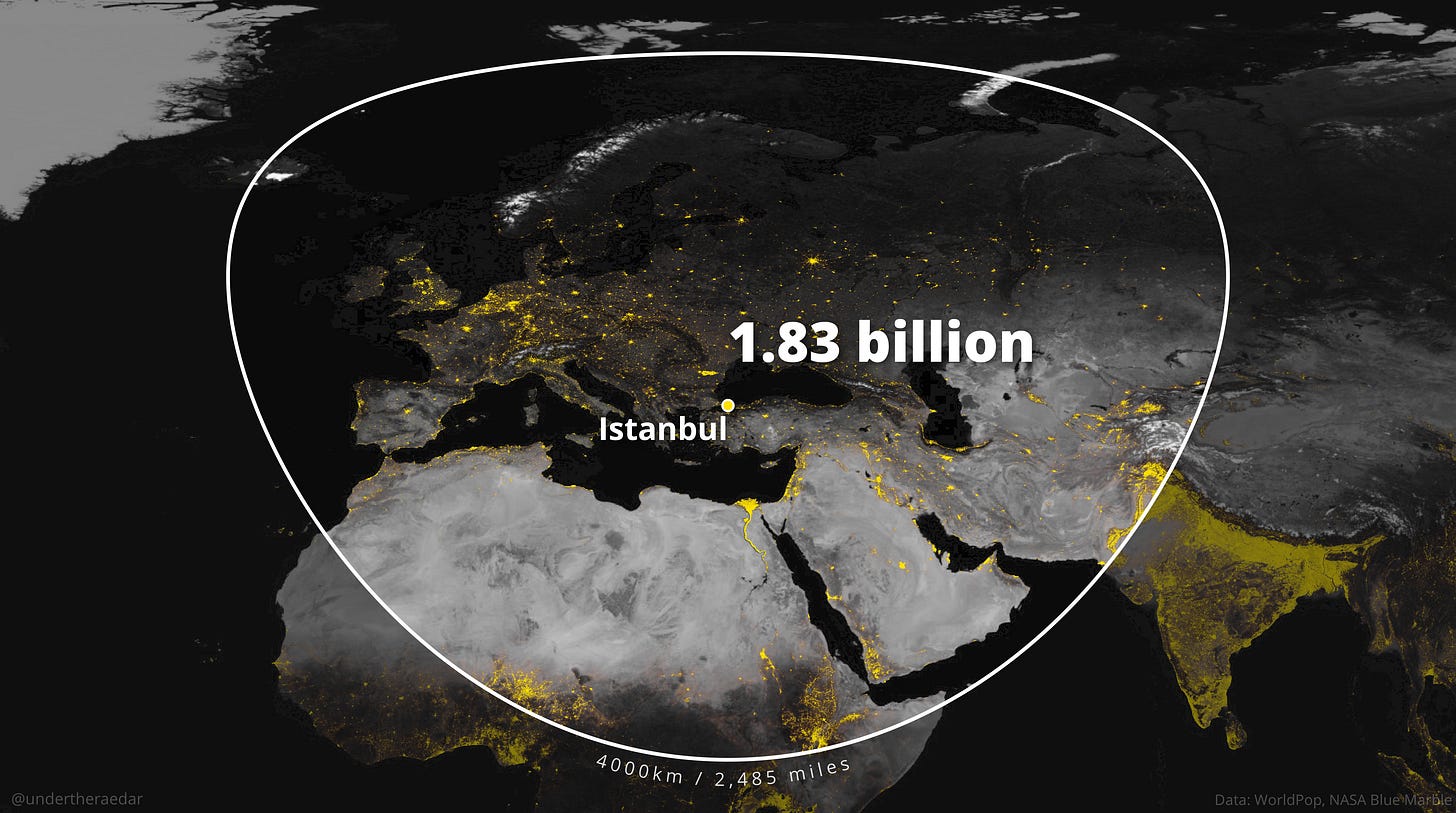
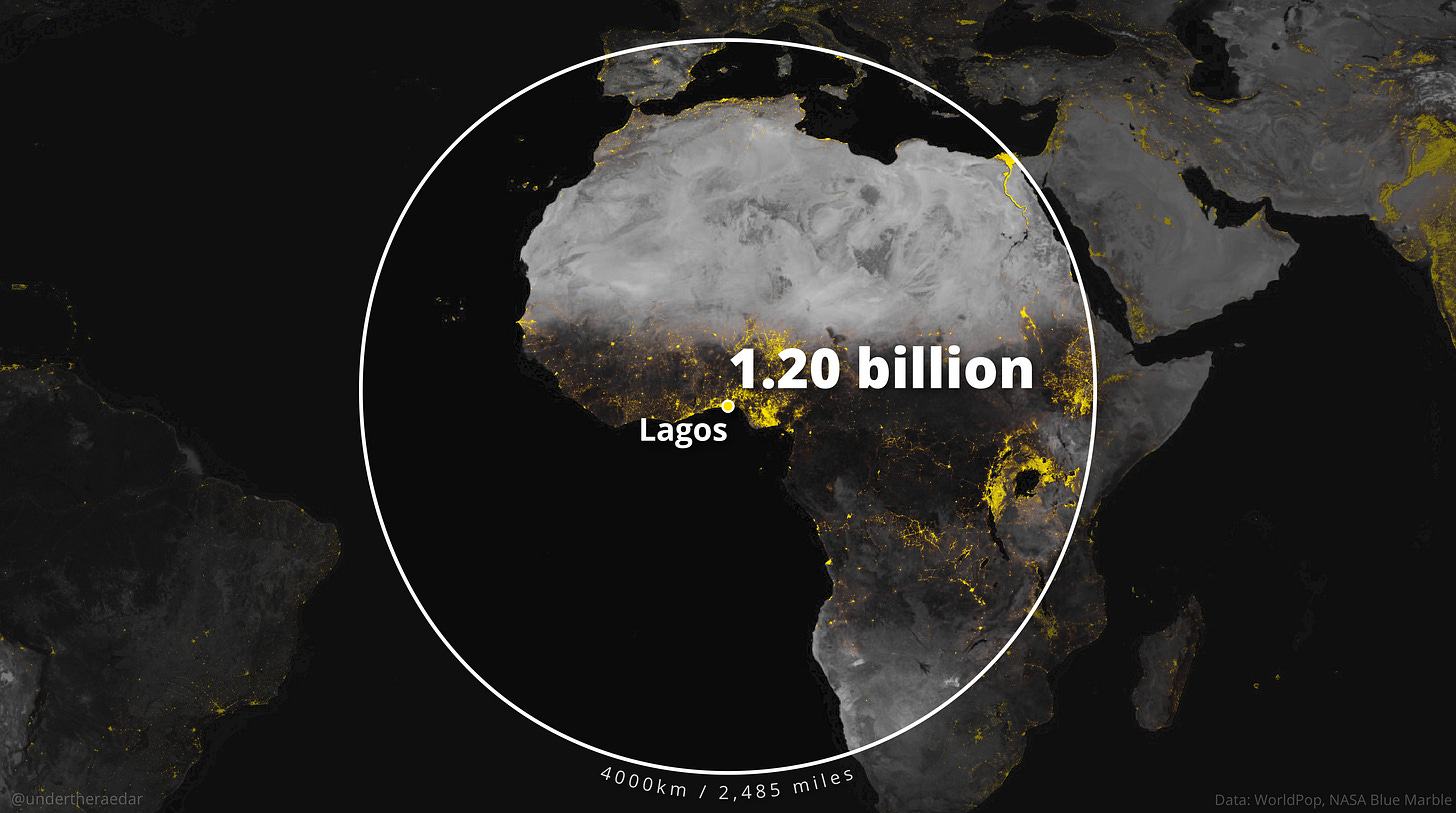
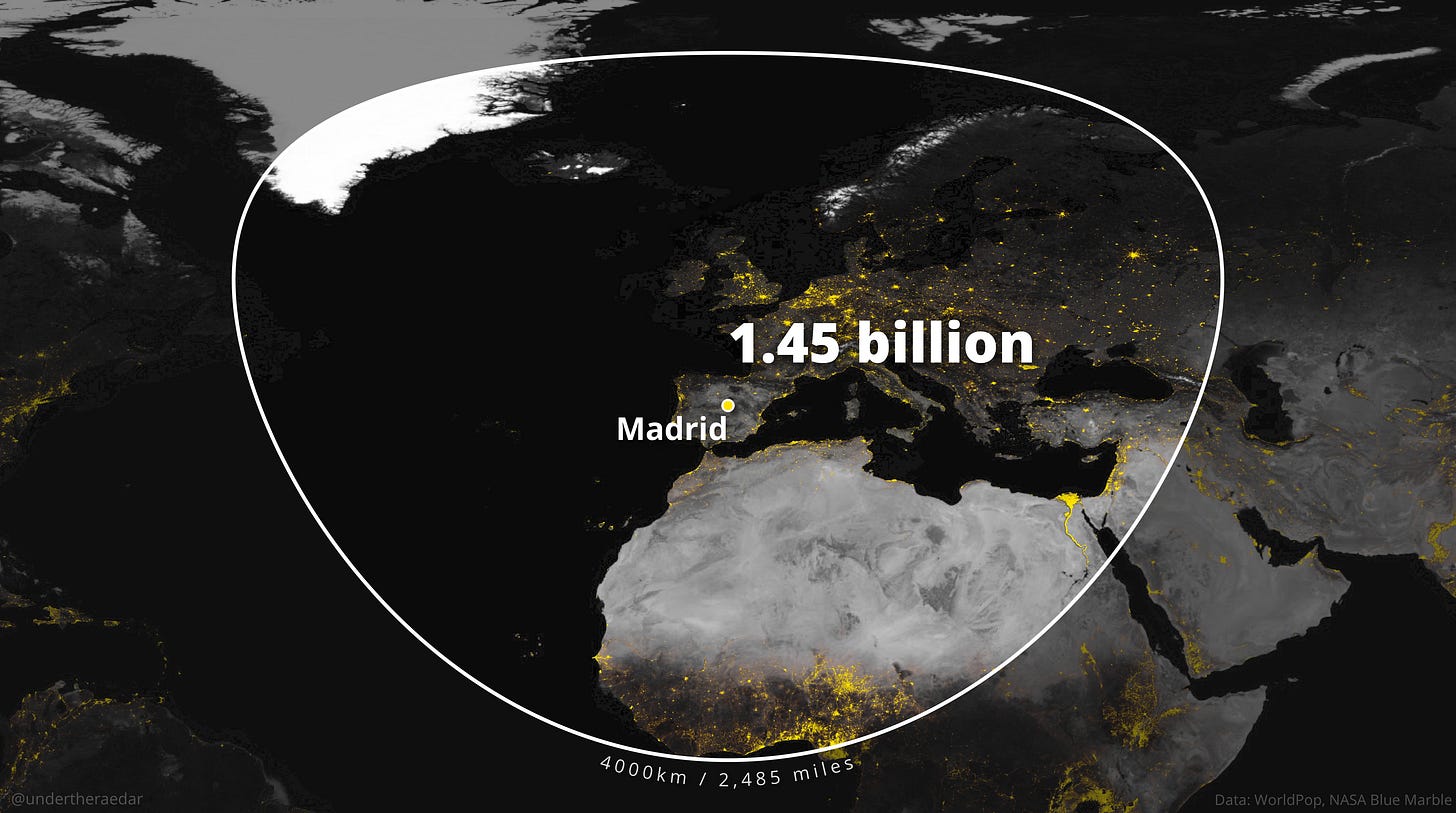
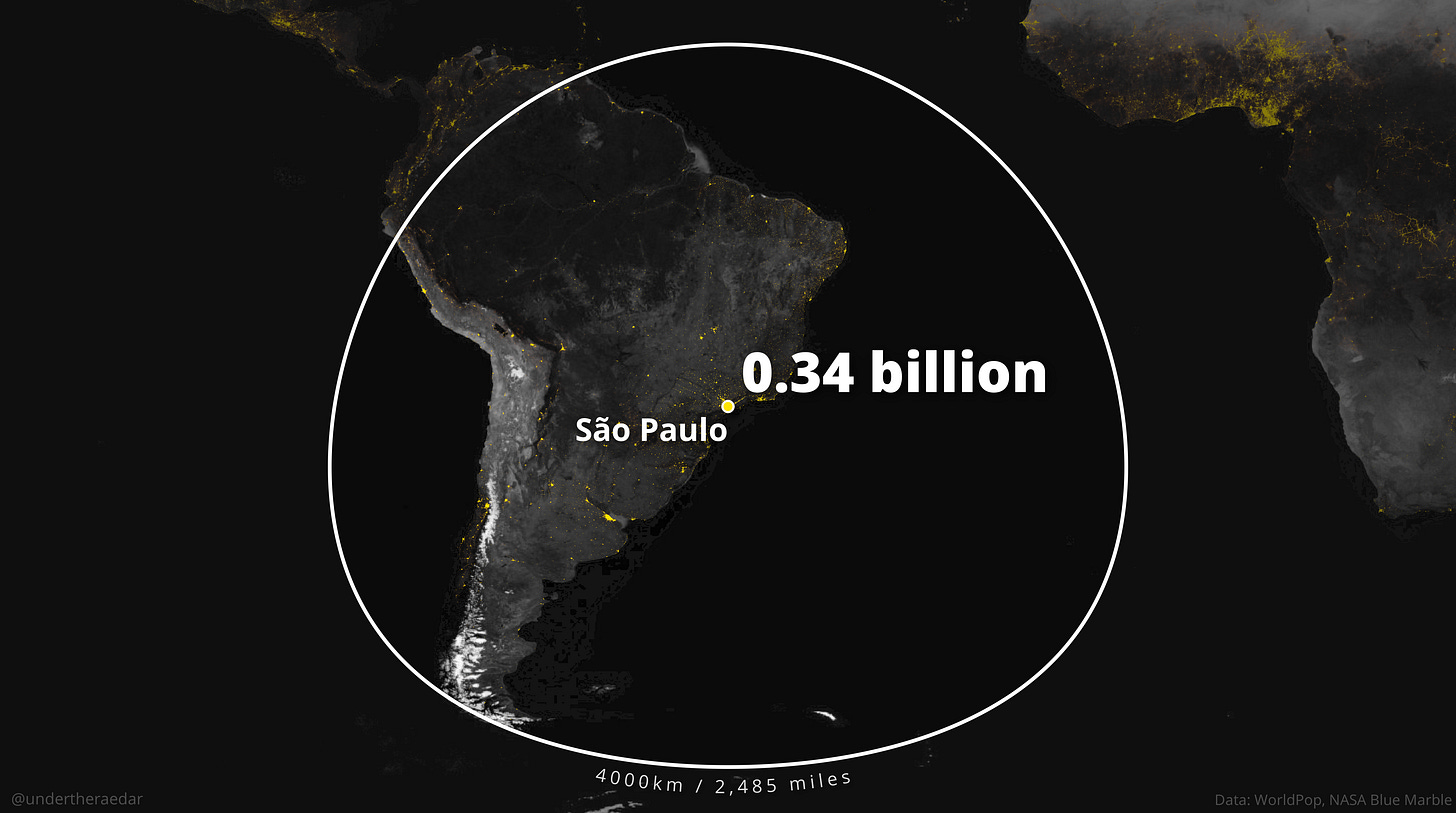
Matemáticas y otros círculos
Como última curiosidad, os quiero traer por aquí también el trabajo de Rudy Arthur sobre el círculo de Valeriepieris y el análisis espacial de datos10. En él, Arthur expande la idea del círculo de Valeriepieris, y crea un algoritmo que permite calcular el círculo que divide los datos de una región en dos partes iguales. A todos los efectos, lo que hizo Danny Quah, pero en esta ocasión de una forma más genérica.
Por supuesto, gran parte del trabajo se realiza sobre la superficie total de la Tierra, pero también dedica una parte a mostrar cómo estos círculos se pueden utilizar para dividir en dos la población de cualquier país. Como, por ejemplo, estos círculos para los distintos países europeos.
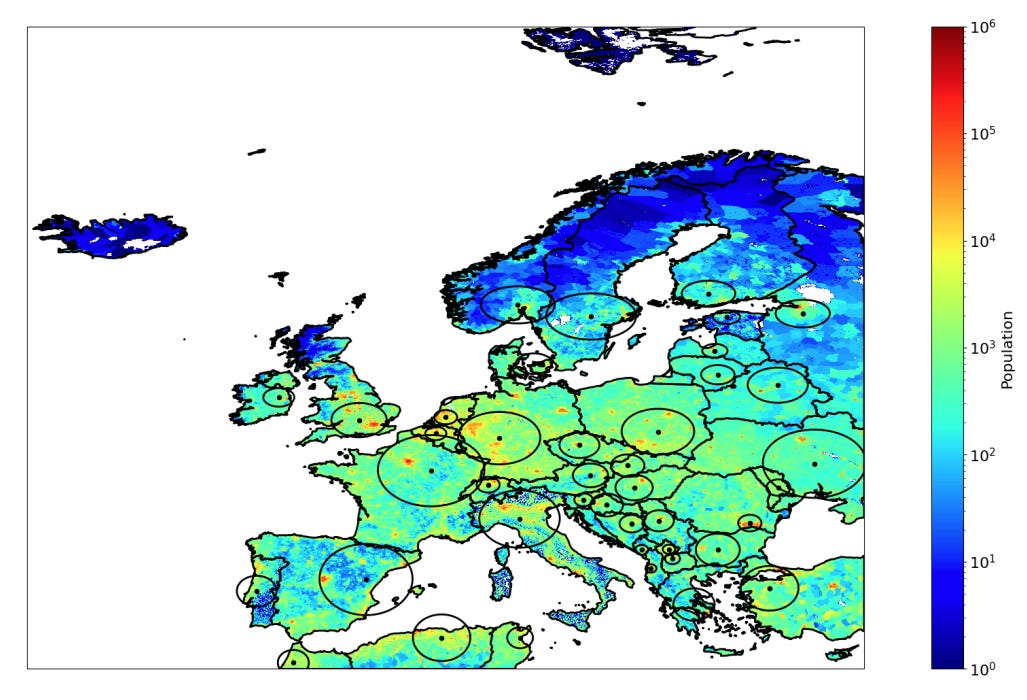
En este mapa, lo que más puede llamar la atención es el caso de España. El círculo es más grande que el de otros países, pero es el único que incluye simultáneamente algunas de las principales ciudades (Madrid, Barcelona, Valencia o Zaragoza), así como una de las regiones más despobladas de Europa, la Serranía Celtibérica.
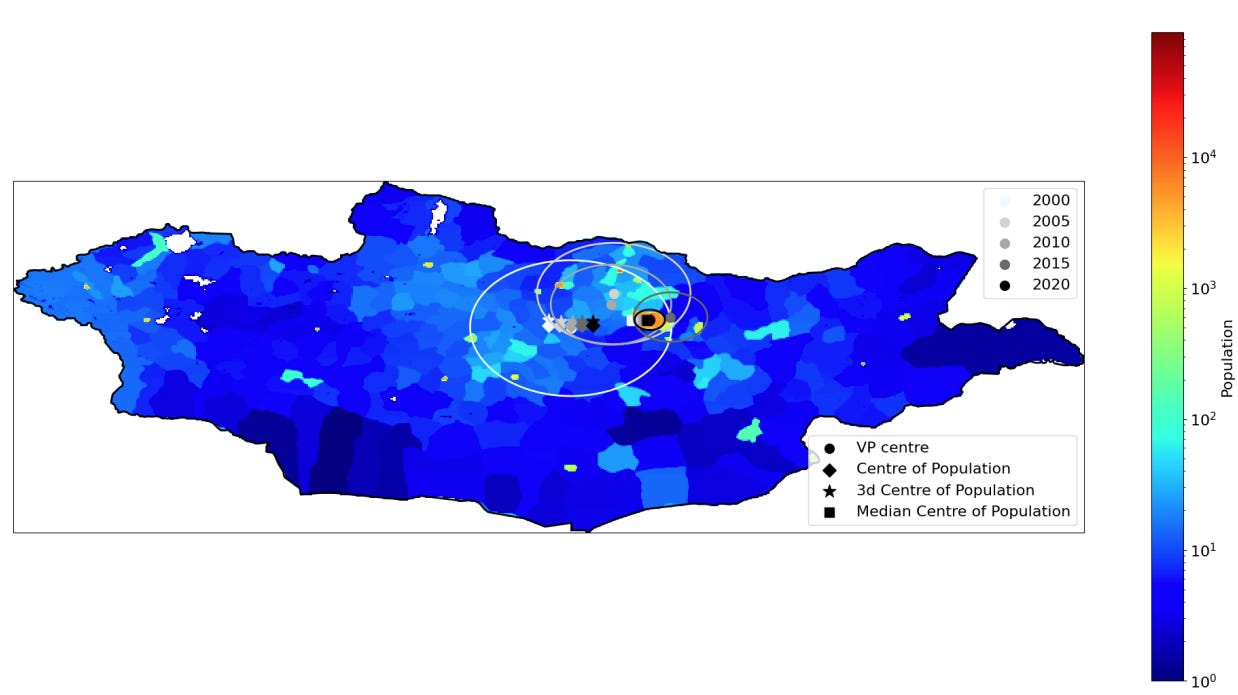
Otra aplicación curiosa de este trabajo es poder observar cómo la densidad de población se va desplazando y concentrando. Especialmente interesante es el caso de Mongolia, donde se puede ver cómo el círculo se va haciendo más pequeño con el paso de los años, hasta concentrarse por completo en la capital, Ulán Bator.
Por petición popular, os dejo por aquí un botón para procrastinar, por si os pillo aburridos. Cada vez que pulséis en él, os llevará a un mapa distinto de los más de 1000 que tiene el catálogo.
Esta fue la entrada que publicó originalmente. Dado que el autor borró su cuenta de Reddit, con ello se fue todo el contenido. Aún podemos encontrar una copia en el Archivo de Internet y también la imagen en Imgur, donde se almacenaban las imágenes de Reddit por aquel entonces.
Estos datos vienen del Censo de los Estados Unidos, tal y como queda reflejado en este artículo del Washington Post publicado un par de días después de que este mapa se hiciera viral.
Y más de la mitad siendo mares y océanos.
Me gusta insistir en algunos temas, así que me repito: el mapa “correcto” no existe.
El crédito, en casi todas partes, se le da a Danny Quah, un profesor singapurense de la Escuela Económica de Londres (LSE). Ken Teoh fue el becario que trabajó con él en todo esto, tal como el propio profesor afirmó cuando publicó por primera vez este trabajo en su blog.
Es increíble lo que ha mejorado la computación en tan poco tiempo.
Alasdair Rae ya ha aparecido por aquí, también al hablar de densidad de población.
A pesar de que la computación ha mejorado entre 2015 y 2022, la principal razón por la que Rae se pudo permitir menos granularidad es porque tenía limitado el número de cálculos a únicamente 1.500 puntos, tantos como ciudades estaba barajando.
Justo en 2022 llegamos a los 8.000 millones de habitantes en el mundo. En la actualidad, octubre de 2025, estamos en torno a los 8.200 millones.
Aquí tenéis el artículo, por si tenéis curiosidad.
Muy interesante como siempre, Miguel. Leyéndote, me venían a la cabeza dos cosas:
1. El contrapunto que se forma entre este círculo de "máxima" densidad de población y el del máximo círculo de mínima población, que supongo que estará muy alineado con el punto de Tierra más alejado de cualquier otro, del que alguna vez nos has hablado en mitad del Pacífico.
2. La evolución que, al estilo de Mongolia, habrá tenido Madrid en España. Tengo curiosidad por saber si el crecimiento y el peso de Barcelona ha impedido que ese círculo se haya ido concentrando y cada vez reduciéndose en torno a Madrid (y su sierra, jejejeje).